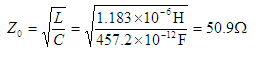特性インピーダンスを測ろう
普段、特性インピーダンス50Ωとか75Ωというのをよく耳にします。
ところで特性インピーダンスとはいったい何なのでしょうか。
…専門的なことは他のホームページや文献にお任せして…(^^;
素人的に書きます。まじめにやっても混乱するだけですので。
ここに、アマチュア無線では良く用いられる50Ωの同軸ケーブルがあります。
50Ωとはいったい何のことでしょうか。Ωって抵抗の単位だけど、テスターで
抵抗レンジにして測れば測れる??
いえ、残念ながら測れません。
試しに芯線と芯線の抵抗値を測ってみてください。…0Ωですね。
では芯線と編線の抵抗値を測ってみると…∞Ω(Over.Flow)。
当然、編線と編線の抵抗値は0Ω。これは、直流の世界では別に
不思議なことではありませんよね。
ということで、テスターで抵抗値を測るように特性インピーダンスを
測ることは不可能であるということが分かりました。
同軸ケーブルは直流も流せますが、もともとMHzオーダーの高周波
を流すためのケーブルなのです。高周波になると抵抗Rだけではなく、
インダクタンス(コイル成分L)やキャパシタンス(コンデンサ成分C)も
考慮しなければなりません。
以下が、同軸ケーブルの等価回路です。
このように抵抗とコイルが直列に、コンデンサが並列に入った構造に
なっています。
テスターで芯線と芯線を測ったときは、直流なのでLに対するリアクタンス
XLは0Ω、抵抗値はほぼ0Ωのため、0Ωとなりました。またCに対する
リアクタンスXcは∞Ωなので、芯線と編線間は完全に絶縁された状態
であったことがわかります。(下記の式に、周波数f = 0Hzを代入)
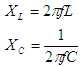
次に直流の変わりに高周波を流してみたらどうなるでしょうか。今度は
f ≠ 0Hzですから、XLが0Ωや、Xcが∞Ωみたいに単純にはいきません。
ここで文献を頼ると、特性インピーダンスZoとは以下の式で与えられます。
ただし、等価回路の抵抗R = 0であることを前提にした近似式です。
芯線は銅で出来ているのでR = 0とおいてもそこそこ近似が出来ます。
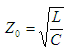
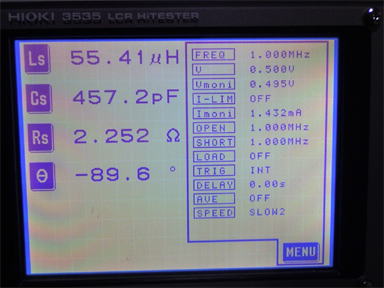
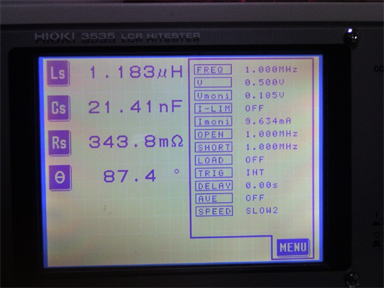
上式より、同軸ケーブルのLとCを測れば特性インピーダンスZoが求められる
ことがわかります。理論は置いといて、とりあえず測ってみましょう!