ここで紹介したいのは「7MHzキラー for 21MHz」すなわち、21MHz帯(使用周波数)への7MHz(不要周波数)の飛込みをカットしてやろうというものです。先ほどの「3.5MHzキラー for 7MHz」と何が違うの?わざわざ別ページにして説明する必要はあるの?と思われるかもしれませんが、なんと前ページの方法では21MHzに対して7MHzはカットすることができないのです。
7MHzキラー for 21MHzは、やっかいだ!
ではなぜやっかいなのかを簡単に説明します。
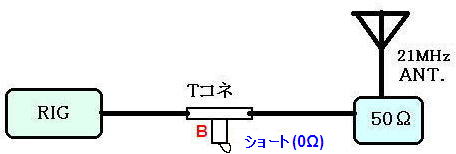
まず前ページの方法でこのフィルターを作ってみましょう。
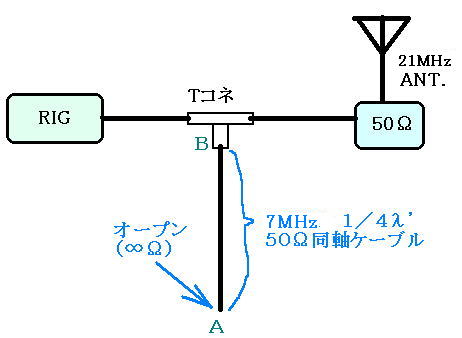
これで、21MHzは通過して7MHzをカットしてくれそうですね。
・・・ちょっと待った!本当にそうなっているのかスミスチャートを用いて
調べてみましょう。
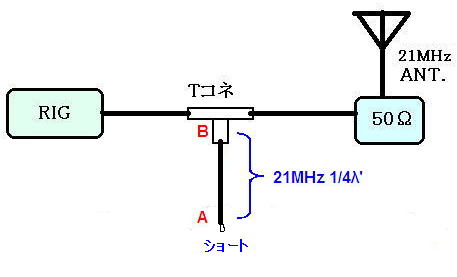
まず7MHzに対するB点(Tコネ直下)でみたインピーダンスZ’を求めます。
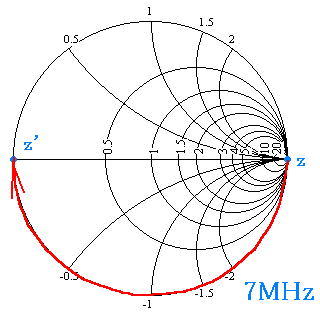
トラップ先端(A点)はオープンなのでz=∞
1/4λ’離れたTコネ直下(B点)ではz’=0(ショート)に見えます。つまりRIG側から見た合成インピーダンスは0Ωになるため、7MHzに対してSWRは∞となり7MHz帯をカットします!なんだちゃんと不要な電波をカットするじゃないか。
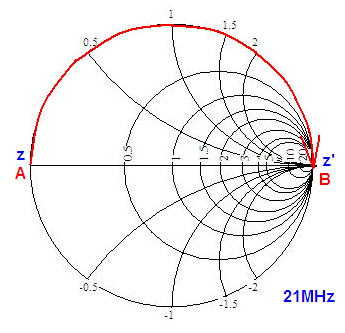
では肝心の21MHzはどうでしょうか。7MHzの1/4λ’のトラップですから、21MHzでは3/4λ’に相当します。1/4λ’あたり半周回転するのでスミスチャートは以下のようになります。
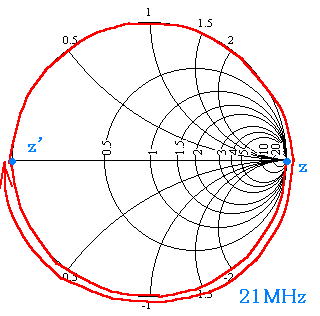
スミスチャートを1周半してz’=0、なんと7MHzと同じインピーダンスになっています!これでは不要な7MHzはカットするけど、必要な21MHzまでSWR=∞で使い物になりません。逆にトラップの先端をショート(z=0)としたところで7、21それぞれz’=∞(SWR=1)になってしまうので、こんどは21MHzは通過するけど、不要な7MHzまで通過してしまいフィルターの役目を果たしません。
※B点での正規化インピーダンスz’=0でSWRは∞、z’=∞でSWR=1に
なることは前ページに記してありますのでご参照ください。
これは困りました・・・
と、普通は途方にくれますが、PSJさんのサイトにこれを見事に解決したトラップがあり、ありがたいことに何も考えずに作って使用すればうまく動作します。ご本人のサイトにも説明がありますが、このサイトではこのフィルターの動作を「スミスチャートを使って」みていきます。
7MHzキラー for 21MHz
以下が、PSJさん設計の同軸トラップです。
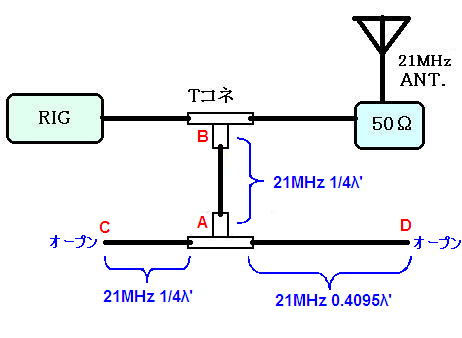
第1段階:基本波の21MHzが通るかの確認。
第2段階:妨害波の7MHzをカットするか確認。
の順にトラップの動作を検証していきましょう。
「第1段階」 このトラップに21MHzを通してみるとどうなるでしょうか。
(1)まずA点のインピーダンスを求めて見ましょう。
A-C間の同軸は21MHzの1/4λ'の長さですので、AのインピーダンスはCのインピーダンス(∞Ω)を半周時計回りに回した0Ω、つまりA点は高周波的にはショートしているように見えます。
| A | 0Ω(ショート) |
| C | ∞Ω(オープン) |
おっと、A-D間の同軸はどうしたかですって?実はA点で高周波的にショートしているのでA-D間の同軸がどんなインピーダンスをとろうが関係ないんです。たとえA-D間が100Ωだろうが∞Ωだろうが、A点のインピーダンスは必ず0Ωなのでここでは無駄な計算をしないことにしましょう。
現時点では等価的にこのように見えています。はじめの枝分かれトラップ
に比べて少し簡単になりましたね。
(2)次にB点のインピーダンスを求めましょう。
先ほど同様、A-B間の同軸は21MHzの1/4λ'の長さですので、BのインピーダンスはAのインピーダンス(0Ω)を半周時計回りに回した∞Ω、つまりB点は高周波的にはオープン(何もつながっていない状態)に見えます。
| A | 0Ω(ショート) |
| B | ∞Ω(オープン) |
ここまでくると分かりやすいですね。はじめの枝分かれ同軸トラップは
21MHzを通したときは等価的にこのように見えます。
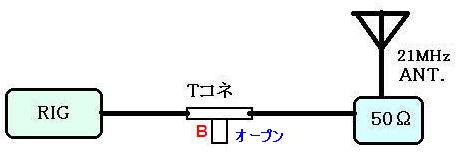
Tコネに∞Ωと50Ωが並列につながっている回路ですので、合成インピーダンスは50Ωとなり、21MHzにおいてはSWR=1で整合していることになります。これで目的の周波数は通過することが確認でき、第1段階終了です。
※計算方法は前のページ参照
「第2段階」 次に妨害波である7MHzを通したらどうなるでしょうか。
(1)まずA-C間の同軸の動作を見てみましょう。
C点ではオープンなのでZ=∞Ω、同軸の長さは21MHzの1/4λ'、つまり7MHzの1/12λ'ですから時計回りに60°回した位置がA点側のインピーダンスZ’となります。
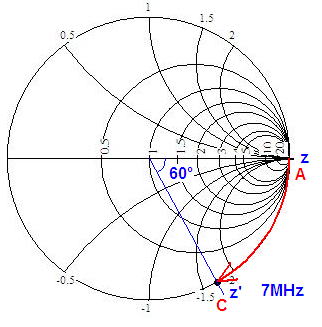
スミスチャートより正規化インピーダンスz’=-1.74j、これに特性インピーダンス50ΩをかけるとA点側のインピーダンスはZ’=-87j(Ω)であることが分かりました。
| A | -87j(Ω) |
| C | ∞Ω(オープン) |
(2)次にA-D間の同軸の動作を見てみましょう。
D点ではオープンなのでZ=∞Ω、同軸の長さは21MHzの0.4095λ'、つまり7MHzの0.1365λ'ですから時計回りに約98°回した位置がA点側のインピーダンスZ’となります。
※ちなみに角度の計算は、1/4λ'(0.25λ')で180°回るんだから
0.1365λ'では
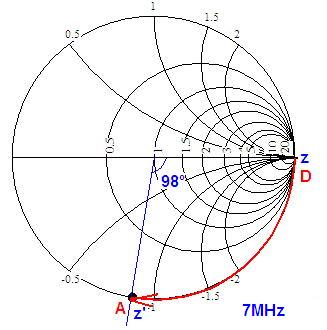
スミスチャートより正規化インピーダンスz’=-0.86j、これに特性インピーダンス50ΩをかけるとA点側のインピーダンスはZ’=-43j(Ω)であることが分かりました。
| A | -43j(Ω) |
| D | ∞Ω(オープン) |
ここまでの結果、7MHzを通したとき元の枝分かれトラップは
等価的に以下のように見えていることが分かります。
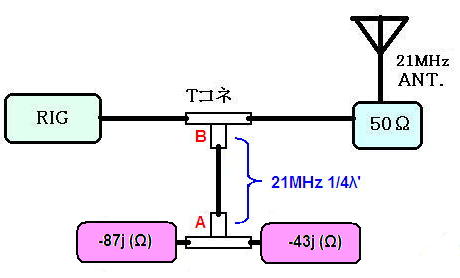
A点には図のように容量性リアクタンス(コンデンサ成分)が並列に接続されているように見えています。ここでA点の合成インピーダンスを計算すると、
つまりA点に-29j(Ω)の負荷がつながっているのと同じことになります(下図)。
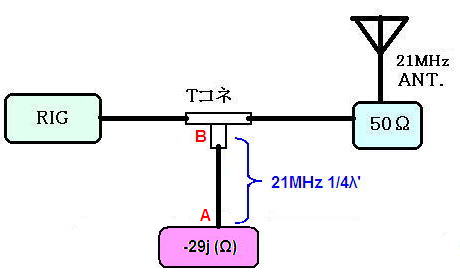
元のトラップに比べだいぶ単純化されてきました。もう一息ですのでがんばりましょう!
(3)最後にA-B間の同軸の動作を見てみましょう。
まずA点のインピーダンスZ=-29j(Ω)を特性インピーダンス50Ωで割って正規化するとz=-0.58となります。これが21MHz 1/4λ'、すなわち7MHz 1/12λ'の同軸を通ることでスミスチャート上を60°時計回りに回ります。
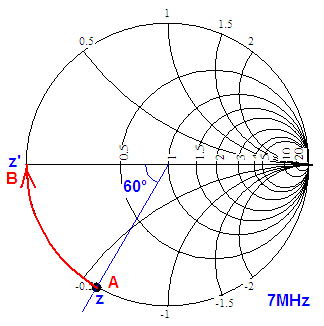
B点のインピーダンスがちょうど0Ωになっています!
ということで長い道のりでしたが、結局7MHzを通す場合は等価的に以下のようになり、SWR=∞と、うまい具合に妨害波をカットしてくれることが分かりました。
以上で同軸トラップの説明は終わりです。最後に触れた7MHzキラー for 21MHzは動作が複雑で難しかったかもしれませんが、同軸トラップの仕組みはちょっとした雑学として頭の隅に残しておいていただければ幸いです。
参考文献:高周波技術センスアップ101 広畑敦著 CQ出版社 pp093-120
参考webサイト:JG7PSJ on the Web! http://www.ganko.tohoku.ac.jp/~psj/tech01.html
使用したスミスチャート描画ソフト:SMITHCHART PLOT for Windows 95/98
※気が向いたら違う周波数のトラップの作り方や例題などを載せるかもしれません。
<<前へ