次へ>>
2.スミスチャートとは
2.1 インピーダンス
高周波回路では直流回路の抵抗(R)のかわりに、インピーダンス(Z)というパラメータを用います。いずれも単位はΩで、電流の流れにくさを示しています。高周波回路では、コイル(L)やコンデンサ(C)も抵抗(リアクタンス)になることはご存知かと思います。
インピーダンス Z=R+jX (Ω)
のように複素数表示をします。コイルやコンデンサによる抵抗(リアクタンス)Xは虚数として表し、実部は純抵抗(直流回路で使われる抵抗そのもの)です。Xは入力信号の周波数によって変わるので、Xが変化するためZが変化します。この周波数によって変わるインピーダンスを図にプロットしたものをスミスチャートといいます。Xは±の値をとりますが、+jXの時は誘導性(コイル的)-jXの時は容量性(コンデンサ的)のリアクタンスです。
2.2 スミスチャート
ごちゃごちゃ文章を読むのはいやでしょうから先へ進みましょう(^^
早速ですが下の図がスミスチャートです。順を追って説明しますので今の時点ではとりあえず眺めておいてください(笑)
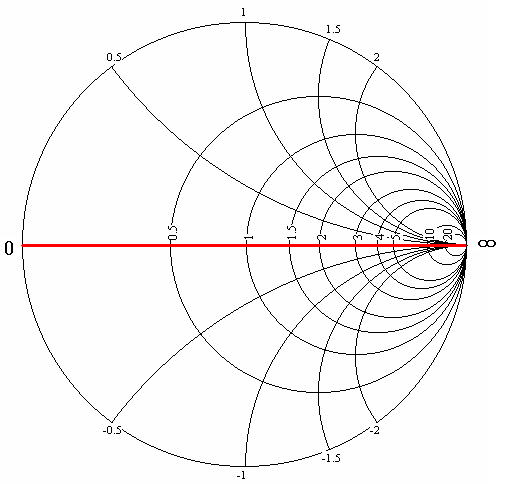
赤い線上が純抵抗Rです。つまりZ=R+jXの「X」がゼロのときです。一番左端が0、右端が∞となっていますね。右へ行くほど抵抗値が高いということです。実はスミスチャート上ではインピーダンスは100Ωのようにそのままの値をプロットしません。インピーダンスZを伝送路(同軸ケーブルなど)の特性インピーダンスZ0で割った正規化インピーダンスを用います。
特性インピーダンス50Ωの例
| Z=150+50j (Ω)のとき |
| ↓50Ωで割る |
| z=3+1j |
通常同軸ケーブルの特性インピーダンスはZ0=50Ωですので、Z=100Ωを正規化すると「z=2」になります。スミスチャート上では、水平軸上の「2」の位置で表されます。(下図)
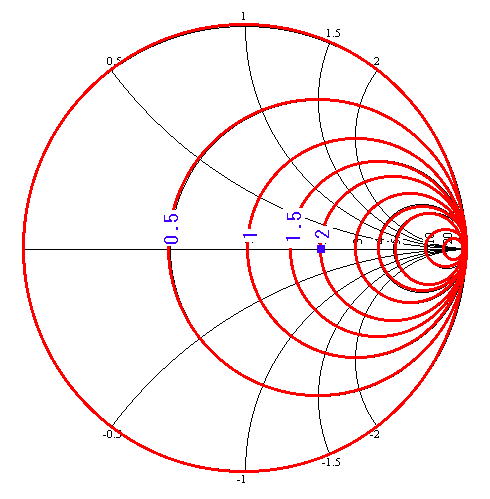
上図の赤で示された円上はそれぞれ抵抗値Rが一定な、定抵抗円です。インピーダンスZ=R+jXの「R」が一定で、「jx」が変化をする場合です。R=100Ω(r=2)の円上は、Z=100+jXということです。(z=2+jx、小文字は正規化された値)
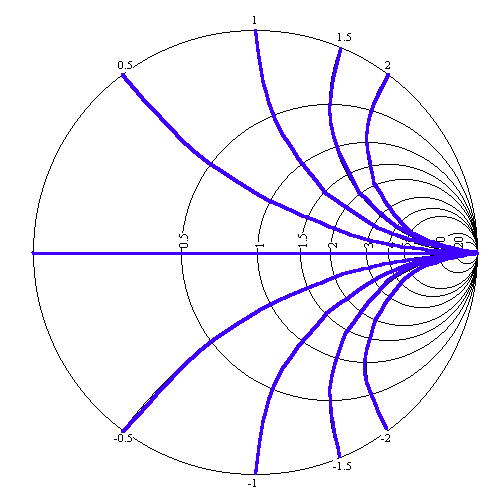
青い線上はそれぞれリアクタンスが等しい、定リアクタンス円です。定抵抗円と逆で、「jX」が一定で、「R」が変化します。例えば、z=r-0.5jです。実は一番初めに書いた純抵抗の赤線ですがこれも定リアクタンス線で、jX=0j一定の線です。
2.3 スミスチャートの使い道
そろそろ眠くなってきたのではないでしょうか?(笑)一応スミスチャートの説明をしましたが、同軸トラップの説明にはあまり必要ない?ような気がしますのであまり分かってなくても結構です。
スミスチャートは、インピーダンスの動きを見るだけでなく、SWRや反射係数、負荷の電圧、電流などをそのまま読み取ることができたり、インピーダンスをアドミタンス(インピーダンスの逆数)に変換したり、いろんなことが簡単にできる便利なものです。ここでは同軸トラップに関係ない説明は省いて簡単に触れたいと思います。興味のある方は書籍で勉強することをお勧めします。
・SWRを読み取る
アマチュア無線をやられている方ならどなたでもご存知のSWR(Standing Wave Ratio)ですが、なんとインピーダンスをスミスチャートにプロットするだけで一発で読み取ることができます。
試しに、特性インピーダンス50Ωに、Z=80ー20j (Ω)の負荷をつないだ場合のSWRを求めてみましょう。
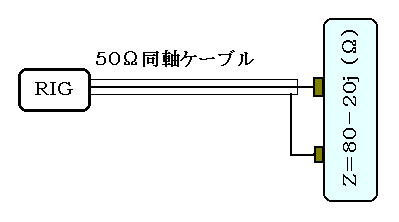
| Z=80-20j (Ω) |
| ↓50Ωで割る |
| z=1.6-0.4j |
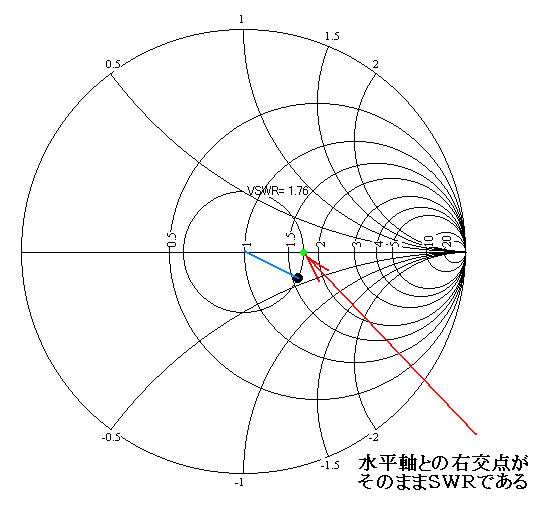
上図は、黒ポツが正規化インピーダンス(z=1.6-0.4j)、1を中心とした円は等SWR円、円と水平軸交点の緑ポツが求めるSWRになります。この場合、SWRは1.5と2の間にあることがぱっと見でわかります。(具体的には1.76弱になります。)まだきちんと説明していませんでしたが、スミスチャートで言う「1」とはZ=50Ω(z=1)のことで、完全に整合が取れた点です。このチャートでは中心部付近にインピーダンスがいるとき、より整合された状態で、外へいくほど不整合度が大きくなります。外周円はSWR=∞の等SWR円です。よく無線機に内蔵されていたり外付けするオートマチックアンテナチューナーは、アンテナのアンテナのインピーダンスができる限り中心に近づくようにバリコンを自動で回して追い込んでくれています。
・同軸ケーブルを通るとインピーダンスが変わる!?
アンテナチューナーでアンテナのインピーダンスを調整してくれると書きましたがあれは厳密にはうそです(え!?)上の例では負荷Z=80-20j(アンテナに相当)ですが、同軸がつながっていますね。通常、アンテナ(負荷)直下とRIG直下ではインピーダンスは異なるのです(例外:負荷Zがぴったり50Ωのときはどこで測っても同じ)。「でも、同軸って5mのものつないでも10mのものをつないでもSWRなんて変わらないよね??」おっしゃるとおりです。インピーダンスは同軸の長さで変わってしまうのですが、SWRはどこでも同じなのです。つまり同軸ケーブルの位置によって、等SWR円上をぐるぐる回ってインピーダンスが変化していくのです。
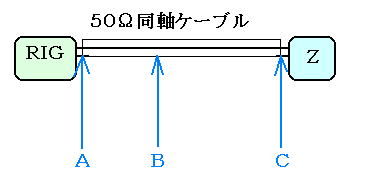
それぞれA,B,C点でインピーダンスを測定すると異なった値が出てきます。逆にいうとRIG直下(A)のインピーダンスを同軸ケーブルの長さによってある程度コントロールすることが可能なわけです。
RIG直下(A)でみたインピーダンスは、同軸ケーブルの長さが1/2波長で一周して元に戻ります。(つまり1/2波長の同軸をつなげばAのインピーダンスはCと等しくなる)以下は等SWR円です。
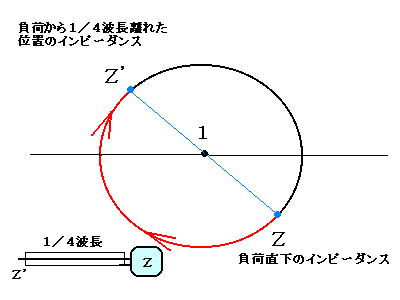
1/2波長で一周するということは、インピーダンスを半周分動かすには1/4波長の同軸ケーブルが必要ということです。このように1/4波長の同軸ケーブルをつなぐと負荷と反対側の端は、時計回りに半周した位置のインピーダンスZ’になります。
注意:
電波は、真空中を伝わるときはおよそ秒速30万kmの速さで伝わりますが、同軸ケーブル内を伝わるときは減速してしまうため、ケーブル内の波長は通常よりも短くなります。上に出てきた1/4波長は、ケーブル内での波長です。この、真空中に比べてどのくらい波長が短くなるかを表すものが「短縮率」と呼ばれるものです。5D-2Vの同軸ケーブルでは短縮率0.67くらいだそうです。この間実測しましたところ0.65でしたので、ケーブルによって多少ばらつきがあるようです。
10MHzの場合
| 真空中の波長λ=30m |
| ↓短縮率0.67をかける |
| ケーブル中の波長λ’=20.1m |
例)負荷Z=100+50j (Ω)に、10.05MHzの高周波を入力する。負荷とRIG(信号元)を5m(1/4λ’)の5D-2V同軸ケーブルでつなげた場合、RIG直下で見るとインピーダンスZ’はいくらになっているか?
解)
まず問題では5mが10.05MHzの1/4λ’(ケーブル内での波長)となっているが、本当かどうか確かめてみる。5D-2Vの短縮率0.67として計算すると、
次に、Z=100+50j (Ω)を正規化する。5D-2Vの特性インピーダンスZ0は50Ωなので、Zを50Ωで割ればよい。
z=2+1jをスミスチャートにプロットし、z=1を中心に等SWR円を描く。z=r+jxより、r=2、x=1であるから、r=2の定抵抗円、x=1jの定リアクタンス円の交点がZである。等SWR円と水平軸の交点が2と3の間にあるので、SWR=2.5程度ということが読み取れる。(実際には2.62弱)
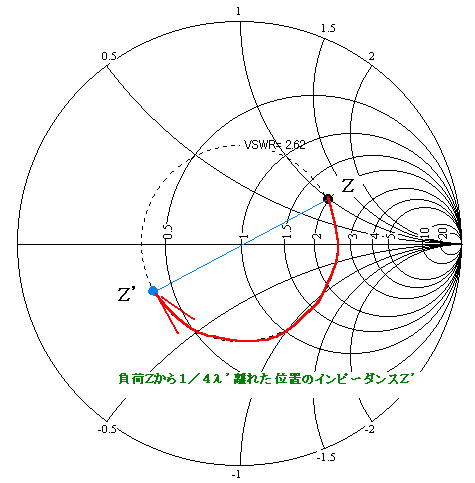
1/4λ’の同軸ケーブルをつないだ場合、インピーダンスは等SWR円の正反対になることは先ほど書いたとおりです。このチャートから、RIG直下で測った正規化インピーダンスを読み取ることができます。うーん・・・ 「z’=0.4-0.3j」ぐらいだろうか??細かい目盛りをふっていないので正確にはわかりませんが、こんなものでしょう。
実際のインピーダンスはZ0=50Ωをかけてあげれば求まるので、
Z’=z’x 50Ω=20-15j (Ω)と求まりました。
ここまで読んでピンと来ない方もいらっしゃると思いますが、とりあえず下図をご覧ください。
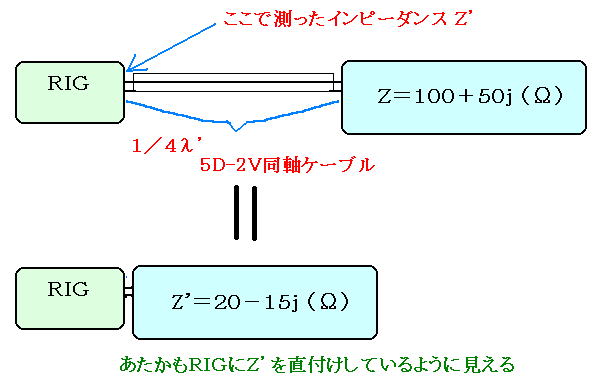
なんとなく雰囲気はつかめましたか?このように同軸の先のインピーダンスと、逆側のインピーダンスが長さによって異なることを利用したのが同軸トラップや、アンテナのスタックに用いるQマッチです。
さらにスミスチャートを使った例題はこちら
<<前へ 次へ>>